GÖDEL’S INCOMPLETENESS THEOREMS

In the previous page I made the case that everything – the universe and all its constituents, the multiverse, and everything beyond – is simply a vast mathematical structure. A complete theory of the universe would actually be the universe itself! The universe cannot completely explain itself purely in terms of the very universe that it is trying to explain. So the language of the complete theory would have to transcend any concepts rooted in our universe, such as energy or elementary particles.
Mathematics is a candidate for such a language. Indeed, papers that attempt to explain ever more fundamental characteristics of our universe, such as those written by the string theorists, are couched in progressively more esoteric mathematics.
If the universe is, indeed, purely a mathematical structure, then it is easier to accept an unimaginably vast number of such parallel universes in a multiverse being generated by mathematical relations that give rise to quantum uncertainty within any given universe (as I described in The Origin of Quantum Probability). These relations (as we saw in Self-Awareness in a Toy Universe), are ultimately based on a few fundamental mathematical truths that we call axioms. I showed how even the processes of simple addition is derived from these axioms.

Axioms lie at the bottom of the food chain – you can’t prove them from anything else. They are the plankton upon which depend small fish like addition and multiplication and, ultimately, out of which, in turn, are constructed the very leviathans of our reality: the axioms that generate our universe and our multiverse and the entire Plexus.
The collection of axioms and mathematical relations that underlie the mathematical structure is called the mathematical system. In this page I shall tell you about an astonishing feature of mathematical systems that use mathematical symbols like “+”, “=” and so on.
If you try to visualize the mathematical structure of the Plexus, you are likely to fail. That is because any picture in your mind is a representation of something in two or three dimensions of space. But space doesn’t contain the mathematical structure of the Plexus – space itself is defined by the mathematical structure, just as space for moving gliders was defined in the previous page by the parameters of the toy universe which was the Game of Life (Self-Awareness in a Toy Universe).
Nevertheless, it is possible to discuss what the properties of the Plexus mathematical structure might be. Take the mathematical structure of the Game of Life. We saw in Self-Awareness in a Toy Universe that different ways of representing the Game of Life were equivalent: (1) a stack of matrices presented in chronological sequence in a computer with “live” and “dead” cells moving about the screen; (2) a diagram showing the rules of the game both pictorially and supplemented with simple clarifying sentences; and (3) the static mathematical structure in Figure 2 of that page.
The common theme of all of these representations is that they are isomorphic in the sense that, if you start with one representation, you can derive any of the others, at least insofar as the essential properties of the Game of Life are preserved. So, while it was easier to imagine a sentient ant with its Universal Turing Machine buzzing away on the computer screen, endowing the ant with self-awareness, that very same self-awareness was nevertheless intrinsic to the static mathematical structure of Figure 2 of Self-Awareness in a Toy Universe.

Although we cannot visualise the Plexus mathematical structure directly, we can make general statements about some of its properties by extending the isomorphism from the generalisations that we can make about familiar mathematical systems.
In Figure 5 of Self-Awareness in a Toy Universe I showed you that, if you add three to a number, the answer is given by applying the successor function Λ to the number three times:
a + 3 = ΛΛΛa
A string of symbols like this is technically called a formula. If the string is a meaningless babble, it is still a formula, but if it has a meaning, then we call it a well-formed formula. If the formula can be produced from the axioms and rules of the mathematical system, then that formula is called a theorem.
The above formula is a theorem because it was produced from Axioms 2 and 3 in Figure 4 of Self-Awareness in a Toy Universe.
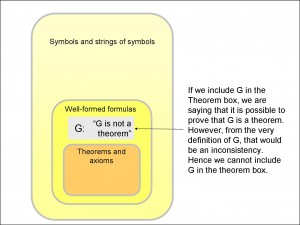
Figure 1 shows the hierarchy of these components of a mathematical system. Notice that some well-formed formulas are not axioms or theorems because you cannot produce them from the system’s rules and axioms. So, for instance, you cannot prove that “Λ0=0” (1 = 0) – your system would be in trouble if it could! The symbol “Λ” was defined in Self-Awareness in a Toy Universe as the successor symbol. It operates on the natural number to its right to produce the next natural number. The “∀” symbol stands for “for all”. It means that every possible value of the symbol to its right is to be included. The tilde sign, “~”, means “it is not the case that”, and “V” means “or”.
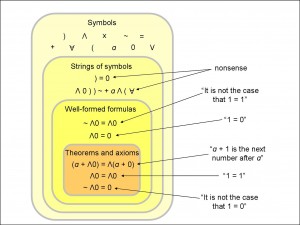
Notice that the last two formulas in the list of theorems look like the two formulas in the box of well-formed formulas, apart from the tilde sign, “~”. This is no coincidence. In general, if a formula can be produced from the axioms and rules of the system, which means that it is a theorem, then putting a tilde in front of the theorem – “it is not the case that” – negates the meaning. It should be no surprise, then, that a theorem that is negated like that gets pushed out of the “Theorems and axioms” box and relegated to the “Well-formed formulas”.
By the way, just as a double negative implies a positive, so does a double tilde “~ ~”. So, when you apply a tilde to the theorem “~Λ0=0” you get “~~Λ0=0”. Since a double tilde implies a positive, you can just ignore the double tilde altogether and so “~~Λ0=0” becomes just “Λ0=0”. This formula, as we see in Figure 1, is a well-formed formula but no longer can be counted as a theorem. I have generalised this in Figure 2.
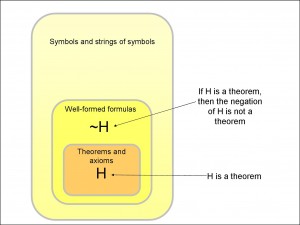
In Figure 2, I started with a formula H that I produced from the axioms and other theorems in the mathematical system (whatever they are) and then I wrote down the opposite formula, ~H, which is the negative of H. Since H can be proved, clearly you cannot also prove the negative of H. Just to take the example above, since “~Λ0=0” can be proved in the mathematical system (“it is not the case that 1 = 0”), it would be absurd if you could prove its negative: “~~Λ0=0” = “Λ0=0” = “1 = 0”. Any mathematical system that could prove the negative of a legitimate theorem would be inconsistent and therefore worse than useless.
But, instead of starting with a theorem and showing you can’t also prove its negative, what about the other way round? Suppose you start with a well-formed formula X, and write down its negative, ~X. One of these has to go into the Theorems and axioms box, hasn’t it? After all, if you write down the formula “Λ0=0” (“1 = 0”) and create its negative “~Λ0=0” (“it is not the case that 1 = 0”), you’d expect that the system could prove one of them (presumably the second!). I have sketched out what I mean in Figure 3.
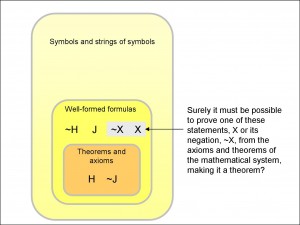
If you look again at the theorems in Figure 1, you’ll see that all three look reasonable: “1 = 1”, for instance. This is because we conventionally interpret a formula that can be proved within the system as being true. So anything within the Theorem and axioms box is interpreted as true. The big question is the other way round: can a true formula always be proved within the system?
How can we be sure of finding a true formula? Well, we can always limit it to one of two formulas. If, for example, formula X is false, then its negative, ~X, must be true, and vice versa. So the question in Figure 3 becomes: since one or other of the mathematical statements X and ~X must be true, can we always prove the true one?
This was a question that was tackled in the early part of the 20th century by the British philosopher, logician and mathematician, Bertrand Russell, who published, along with his mentor, Alfred North Whitehead, three substantial tomes collectively entitled Principia Mathematica.
These three celebrated, momentous volumes attempted to lay out the very foundations of mathematics. Central to this work was an ambition to define a set of axioms and rules from which every mathematical truth could be derived. In terms of Figure 3, since every well-formed formula, call it X, has a negation, call it ~X, Russell and Whitehead set out to construct a mathematical system powerful enough to ensure that, in every case – for every conceivable pair of well-formed formulas X and ~X – one of them would be provable from the axioms of their system and would therefore be included in the box of theorems (and so, by definition, would also be true).
It would, of course, be disastrous for both of the statements of the X, ~X pair to be provable as two contradicting theorems – that would mean that the mathematical system was inconsistent and could not be trusted. Nevertheless, Russel’s and Whitehead’s contemporaries considered the alternative proposition to be equally heinous – that neither statement of such a pair might be provable, that neither might be a theorem. Since either one or the other of the pair had to be true (because one is the negation of the other), then that alternative proposition would amount to saying that the mathematical system would contain a true statement that it couldn’t prove.
The edifice that Russell and North Whitehead had so painstakingly created was demolished in 1931 by a young Austrian logician and mathematician, Kurt Gödel, just after receiving his doctorate in the previous year.
Gödel had become interested in the very same question that had so exercised Russell and Whitehead, and that was continuing to grip the finest minds in mathematics: are the axioms – the basic definitions – in a given mathematical system sufficient to derive every true statement in the system?
How Gödel brought the house down
Gödel delivered his coup de grâce in 1931, in a paper entitled “On Formally Undecidable Propositions of Principia Mathematica and Related Systems”.
In this landmark paper, he showed not only that the mathematical system in Principia Mathematica failed to prove every true statement, but also that any sufficiently powerful, consistent mathematical system must fail also.
In the rest of this page, I am going to sketch out what Gödel did, but only superficially. His paper is long and complicated, and includes notation unfamiliar to modern eyes which is candidly difficult to keep track of. Although I have read his paper many times, it was only through studying more modern proofs of the theorems that I was able to get even the gist of the original! These newer interpretations vary in their intelligibility: the greater the clarity, the less the rigour.
Essentially, what Gödel’s paper says is summarised in the next three figures.

The culmination of Gödel’s paper is to produce a mathematical statement which we shall call G (for Gödel) and the translation of which, in English, is “G is not a theorem”. The question is, should this statement be in the theorem box or outside it (see Figure 4)? If it is a theorem, then, by definition of a theorem, it must be possible to derive G. However, that would mean deriving a mathematical statement that says that G is not a theorem, and, hence, cannot be derived. So we should have an inconsistency. So G cannot be a theorem if the mathematical system is consistent.
What about the negation of G, ~G ? Figure 5 outlines the position. The negation of G effectively states that G is a theorem. So, if we include ~G as a theorem, we are saying that it is possible to prove ~G; that is, it is possible to prove that G is a theorem. However, remember that the meaning of G is that G is not a theorem. So to include ~G as a theorem would again be an inconsistency: ~G cannot be included in the theorem box any more than G can.
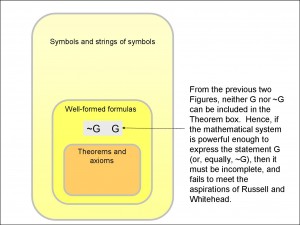
Figure 6 is the combination of the previous two figures and you can compare it with Figure 3 which showed what Russell and Whitehead were trying to avoid: a mathematical statement and its negation both being excluded from the box of theorems. Since one or the other of G and ~G has to be true, then, if the mathematical system is powerful enough to be able to express G and ~G, and if it is consistent, then there is at least one truth which it cannot derive, which makes it incomplete.
It may not be difficult, at first blush, to imagine that it will be a straightforward task to translate the statement G into a well-formed formula using the chosen mathematical system. It’s actually fiendishly complicated, which is why Gödel’s original proof is so hard (at least for me!) to understand. This is because, while it is relatively simple to construct axioms or theorems for most things you might want to do in a mathematical system, G has the property of self-reference, as you will have gathered if you followed the arguments in the last three figures. That seriously raises the game plan.
Gödel’s First Incompleteness Theorem
So what I have done is to use the next four figures to draw Gödel’s demonstration in terms of the way I understand it, missing out the many pages of rigorous definitions and additional mini-proofs that he develops. While my take on Gödel’s theorem is not rigorous, I sleep well knowing that the finest mathematical minds have tried to fault his original paper without success for the better part of a century.

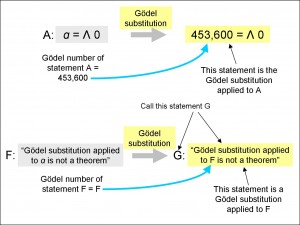
One of the first things that Gödel did was to devise a coding system for the symbols in the mathematical system. In Figure 7, I have followed his coding device fairly closely, except that I have changed the numbers around a little so that the final code number is not too large.
At the top left of the figure, you see the beginning of a list of symbols with a code number allocated to each. The example string of four symbols, α = Λ0, is then encoded using the allocations on the list, with a sequence 5, 4, 2, 1 in this case. Next, we take the first prime number, which is 2, and multiply it by itself 5 times (the first code number in the sequence). We take the next prime number, 3, and multiply it by itself 4 times (the next code number in the sequence). We do this for all four symbols in the string and then multiply everything together to get 453,600 as you can see in the figure. This is called a Gödel number.
Doing it in this way has two advantages. The first is that you can encode not only a string of symbols like the four in the figure: you can encode a whole series of such strings, and that series could be, for instance, all the steps from an axiom to the final step, the theorem that you are trying to prove. So Gödel is able to use this concept to “talk” about theorems and their provability in a precise, unambiguous way.
The second advantage is that you can always decode a Gödel number to yield the original string or theorem. First, you identify the prime factors of the number and arrange them in ascending order of magnitude. Then you count how often each prime number appears in this list and that number is the code of the corresponding symbol. For instance, given 453,600, you turn that into 2x2x2x2x2x3x3x3x3x5x5x7, count the 2’s (5), count the 3’s (4), count the 5’s (2) and the 7’s (1). So the code was 5, 4, 2, 1, getting us back to the original string.
Now, parting further from the detail in Gödel’s paper, but preserving the spirit, we define an operation which I have called Gödel substitution. A Gödel substitution applied to a statement A means replacing the variable “α” wherever it appears in statement A with the Gödel number that you calculate for statement A before you do the substitution. You can see the effect of this in Figure 7, where “α” has been replaced by the Gödel number of statement A, 453,600.
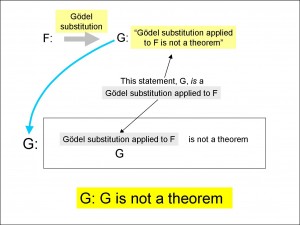
I have re-drawn this Gödel substitution in the top half of Figure 8. In the lower half of the figure, I have written a statement called F that says “Gödel substitution applied to α is not a theorem”. We can calculate the Gödel number of this statement and label it “F”. You can label a statement with anything you like, so we choose to label the statement with its own Gödel number. So, when we apply the Gödel substitution to F, replacing “α” with the Gödel number, F, we get “Gödel substitution applied to F is not a theorem”. Call this statement “G”.
The lower half of Figure 8 is summarised at the top of Figure 9.
In this figure, I have emphasised the fact that the statement G is, in fact, the Gödel substitution applied to F. This, of course, is self-referential, since the statement G talks about this very substitution. G is, indeed, talking about itself!
To help you see that, I have reproduced the statement G in the box in Figure 9, separating it into two parts. The first part is “Gödel substitution applied to F”, which is exactly what G is, and the second part is the remainder of the statement of G, namely “is not a theorem”. So G appears twice: firstly, as the label of the statement that is inside the box, and secondly, as the part of the statement in the box that refers to the process by which it was generated (the Gödel substitution applied to F).

This is the elusive self-reference that Gödel’s genius was able to pin down rigorously: the fact that G is the label of the statement and that the statement talks about G means that the statement refers to itself. The statement is summarised in the lower part of Figure 9: “G is not a theorem”. This is the statement that we were after: the statement G which, as we saw in Figure 6, could not be a theorem any more than its negation, ~G.
It only remains for me to specify the statement G more explicitly. You can see how to do it in Figure 10, where the components of the statement “G is not a theorem” have been spelt out, producing, finally, G: “Gödel substitution applied to ‘Gödel substitution applied to ɑ is not a theorem’ is not a theorem”. That’s it! That is the celebrated Gödel statement in Gödel’s First Incompleteness Theorem.
Gödel’s genius was not only in finding a way to express a statement that refers to itself, but to do so using pure mathematics. (Effectively, his paper follows Figures 7 through 10 using mathematical notation – some of it invented by himself.) Indeed, using his Gödel numbering, the Gödel statement may be expressed as a single natural number.
Gödel’s Second Incompleteness Theorem
Gödel’s Second Incompleteness Theorem follows almost immediately. Effectively, this theorem states that a mathematical system cannot prove its own consistency. We saw above that G cannot be a theorem of the system if the system is consistent. In other words, the consistency of the system implies that G is not a theorem of the system. Since what we have just said – that “G is not a theorem of the system” is a statement of G – then we see that the consistency of the system implies G.
However, if one statement implies a second statement, and the first statement can be proved, then the second statement can be proved. So, if the consistency of the system can be proved, so can G. But we know, from Gödel’s First Incompleteness Theorem that G cannot be proved within the system. Therefore, it follows that neither can the consistency of the system be proved within the system. A system cannot prove that it, itself, is consistent (unless, of course, that system is inconsistent!).
We don’t of course, have to hand ready-made mathematical symbols for “Gödel substitution applied to” or “is not a theorem”, but, in principle, these can be relatively easily added to a sufficiently powerful mathematical system. The point is that any such powerful mathematical system can support true statements that the system is nevertheless not able to prove. In essence, this means that there is at least one true statement in the system that cannot be proved to be true, because either G or ~G must be true. In fact, there is an infinite number of such statements in such a mathematical system – in the first place, you can choose an infinite number of different coding systems that will yield an infinite number of Gödel statements.
Why have I bothered to tell you about Gödel’s incompleteness theorems? We shall see in the next page that they imply a hierarchy within a mathematical system, and that this hierarchy provides the mathematical infrastructure for the multiverse of block universes, resulting in our familiar quantum uncertainty. And it will, at last, afford us at least a glimpse of the very summit of the Plexus.
Click here to go to Mathematical Structure of the Plexus [18]
Save
