TREE STRUCTURE OF THE MANY WORLDS INTERPRETATION

1. “Splitting” in the Many Worlds Interpretation
In spite of the advice of his doctoral thesis advisor, John Archibald Wheeler, to remove the loaded references to “splitting” from the draft of his PhD thesis, Hugh Everett III managed to retain one mention of the word, in the context of the observer, in the finished work:
“As soon as the observation is performed, the composite state is split into a superposition for which each element describes a different object-system state and an observer with (different) knowledge of it.”
As I said in Many Worlds, Everett introduced what was later to become known as the Many Worlds Interpretation (MWI) in order avoid the difficulty of wave-function collapse. In the Many Worlds page, you saw the kind of splitting that Everett envisaged. I have drawn a slightly more general example in Figure 1 here.
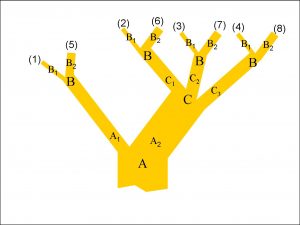
There are three quantum events in the figure, labelled A, B and C. Sometimes I shall call these events “experiments” in the cause of tradition. The outcome of each experiment is labelled by a subscript. So, for instance, the outcome of experiment A may be either A1 or A2.
You can see different possible sequences of events in the figure. For example, in one sequence, outcome A2 is followed by outcome C1, which, in turn, is followed by outcome B1. Eight different sequences are represented in the tree, and I have shown these schematically in Figure 2. I have drawn each of the eight possibilities within a Minkowski block universe (see the Block Universe page). Alice, Bob and Cleo conduct the experiments A, B and C respectively.
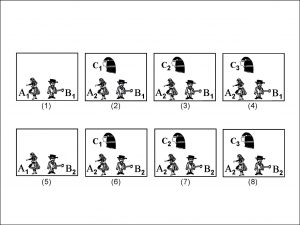
The sequence A2, C1, B1 mentioned above is contained in universe (2), and if you check Figure 1 carefully, you will find that the remaining seven sequences are also each represented in Figure 2. The numbers in brackets at the ends of the branches (the “twigs”) in Figure 1 correspond to the universes listed in Figure 2. So, in a sense, the MWI tree in Figure 1 is isomorphic with the collection of block universes in Figure 2. Notice that experiment C only happens if the outcome of experiment A is A2 and not A1, which is why Cleo does not appear in universes (1) or (5). (Also, for the sake of generality, I have drawn three branches emerging from event C instead of two.)
As you saw in Figure 2 of the Parallel Block Universes page, a feature of MWI trees is that they may be drawn from the perspective of a particular observer. The tree in Figure 1 here captures Alice’s experience. We suppose that Bob is sufficiently far from Alice, spatially, that she sees the result of the experiment performed by Cleo, who is spatially close to her, before Bob’s light-cone can reach her (see Figure 3 of Many Worlds for a discussion of light-cones.)
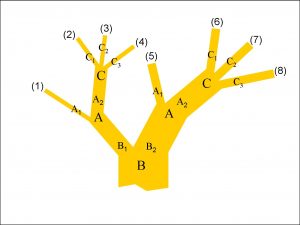
Notice that Figure 1 features the same experiment B four times. If I had drawn the tree from Bob’s perspective instead of Alice’s, I would only have needed to show experiment B once, but A and C would each appear twice – see Figure 3.
Again, if you check the figure, you will see that it contains all of the experimental sequences in Figure 1 – as seen in this case from Bob’s perspective. Once more, this tree is isomorphic with respect to the eight possible sequences of outcomes of the three events in the collection of block universes in Figure 2. As before, I have labelled the ends of the branches with the numbers in brackets that correspond to the eight possibilities in Figure 2.
Since the different perspectives of the MWI tree are isomorphic to the same collection of block universes, in a sense, you can regard the block universes as being a more fundamental representation. I shall come back to this point below.
Regardless of Wheeler’s nervousness over the “splitting” term, you can see clearly from the shapes of the trees that separate branches higher up the tree share common “ancestor” branches. For instance, in Figure 1, the two “twigs” labelled (2) and (6) share the same branch C1.
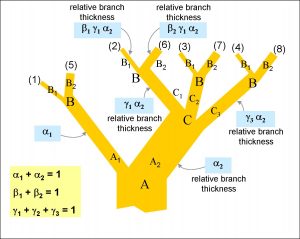
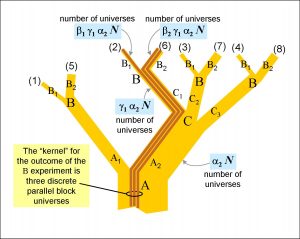
How thick are the branches? In Figure 4 I have indicated the thicknesses of some sample branches using Greek letters in the light-blue squares. The rule is that the thickness of each branch is proportional to the probability of the outcomes of the sequence of experiments leading to that branch.
Let me take a specific example. Experiment A has two possible outcomes, A1 and A2. Let α1 be the probability that the result of the experiment will be A1 and let α2 be the probability that the result is A2. (For enthusiasts of quantum mechanics, α1 is the absolute square of the probability amplitude for outcome A1, and so on.) Since there are only these two possible outcomes, the sum of α1 and α2 must be unity – there is a 100% probability that the result is either one outcome or the other. Just suppose, for example, that α2 is 75%, that is, ¾. Then what is the likelihood of the sequence of experiment A yielding an outcome of A2 followed by experiment C yielding an outcome of C1?
Let γ1 be the probability that the result of experiment C is C1 (and γ2 for C2 and γ3 for C3). Suppose that each of the results C1, C2 and C3 is equally likely. Since γ1 + γ2 + γ3 = 1, then γ1 = γ2 = γ3 = ⅓. So the probability of experiment C yielding an outcome of C1 is ⅓. So the probability of the sequence of outcomes A2 followed by C1 is ⅓ × ¾ = ¼. In other words, it is the product of the probabilities for each branch, γ1 α2.
We can work our way up through the branches applying this process to find the thickness of each new branch in turn. So, in Figure 4, if the outcomes of the B experiment, B1 and B2, have probabilities of β1 and β2 respectively, say, ⅓ and ⅔, then the branch thicknesses are 1/12 and 1/6.
Notice that the branches become thinner as you move upwards through the tree, because the thickness of each branch is only a fraction (which is less than unity) of the thickness of its immediate predecessor.
2. Reconciling the topologies of MWI and the block universe
The characteristic splitting in the MWI tree is not allowed by the block-universe view of Minkowski space. (I should point out here that some physicists still find it difficult to accept the idea of a block universe, which is why I wrote the paper on an experimental test of the block universe.)
As we saw in Parallel Block Universes the way to reconcile the MWI-tree topology with the block-universe topology is to replace the tree with individual, parallel filaments that tend to share a common history towards the trunk of the tree and diverge higher up. These filaments represent block universes. Figure 5 shows a sample of three block universes shaded in brown, one being block universe (2) and two being block universe (6), taken from Figure 2.
In the MWI, observers in twigs (2) and (6) shared the same ancestor branches, C1 and A2. However, in Figure 5 the three observers’ experiences of these previous experiments are identical but separate, because there is a copy of these branches in each of the separate, discrete block universes. It is, perhaps, fitting that the resolution of the topology problem is solved by using a collection of parallel block universes which, as I mentioned in the previous section, is, in a sense, a more fundamental representation than the tree, since it is unchanged by an observer’s perspective.
It will be useful to ask the question: how many parallel universes are there in the multiverse?
In Figure 3 of the Parallel Block Universes page, we saw that if there is a preponderance of parallel universes with a version of you observing a particular outcome (in that case, six universes where both Alice and Bob found the same spin), then that is a measure of the quantum probability of that outcome. So the number of parallel block universes in a branch is proportional to the thickness of the branch.
Suppose that the constant of proportionality is N, so that we find the number of universes in any branch by multiplying the relative branch thickness for that branch (taken from Figure 4) by N. So the number of universes in each of the (2) and (6) branches is β1 γ1 α2 N and β2 γ1 α2 N respectively. Then, since β1 + β2 = 1, observers in a fraction β1 of all of the universes in these two branches will see an experimental outcome B1, and, in a fraction β2, observers will see the outcome B2. Of course, the quantum uncertainty experienced by the observers arises because they do not know which universe they are in.
It is a feature of MWI trees that the total sum of the probabilities of all of the branches is conserved. To see this, note that the sum of probabilities of the eight twigs (numbered (1) – (8) in Figure 5) is (taking the twigs in numerical order):
α1 β1 + α1 β2 + α2 γ1 β1 + α2 γ1 β2 + α2 γ2 β1 + α2 γ2 β2 + α2 γ3 β1 + α2 γ3 β2 = 1
(because α1 + α2 = β1 + β2 = γ1 + γ2 + γ3 = 1)
So long as the number of universes in every branch is proportional to the probability for that branch, the fact that the total of the probabilities is constant (unity) guarantees that the total number of universes in the multiverse remains constant despite the branching (as it should). Furthermore, since the probability of the beginning of the trunk of the tree must be unity (or it would not exist), the number of universes at that beginning must be unity multiplied by the constant of proportionality, N, which is just N. So, in conclusion, the number of universes in the multiverse is the proportionality constant that is applied to every branch, namely N.
3. The number of universes in the multiverse
Is there a lower limit to N? We start by considering the number of universes needed to represent the outcomes of individual experiments. The ratio of the thicknesses of the branches from an individual experiment must be the same as the ratios of the probabilities for each of the possible outcomes of that experiment. So, for example, if outcome B2 is twice as likely as that of B1, then β1 must equal ⅓ and β2 must be ⅔. Therefore, the smallest number of universes that could represent this experiment alone, not considering any other experiment in the multiverse, is 3, with one universe allocated to the B1 outcome and two to the B2 outcome. Recall that we used the term kernel in the Origin of Quantum Probability page for the smallest group of parallel universes that corresponds to a particular experiment. Then the kernel for the B experiment contains three universes: KB = 3, with one in the B1 branch (KB1 = 1), and two in the B2 branch (KB2 = 2).

Taking another example, if the probabilities for the outcomes C1, C2 and C3, namely, γ1, γ2 and γ3, are (1/3), (1/5) and (7/15) respectively, then the smallest group that reflects these probabilities has 5, 3 and 7 universes in these respective branches. You see the pattern? The number of universes in each branch of a kernel is given by multiplying the probability for each of the experimental outcomes by the lowest common denominator (LCD) for the probabilities of each outcome. In this instance, the LCD of (1/3), (1/5) and (7/15) is 15 and the numbers of universes are (1/3) × 15 = 5, (1/5) × 15 = 3, and (7/15) × 15 = 7 for the respective outcomes. So KC = 15 with KC1 = 5, KC2 = 3 and KC3 = 7. I shall talk about the general case, where the probability of an outcome cannot be expressed as a rational fraction, in The Finite Multiverse.
In order to preserve the proportionalities of branch thicknesses for any given experiment, the number of universes in the trunk of the tree has to be the product of the kernels of every event in the tree. Then, proceeding upwards along the branches, the kernel for each experiment is divided into its components according to the relative thicknesses of the branches for that experiment. You can see how this works in Figure 6.
From this, it is clear that the smallest possible number of universes in the multiverse, using the smallest possible number for each experiment (its kernel), is the product of the kernels of all of the experiments that take place in the multiverse. Notice that the repeated appearance of the same experiment on unconnected branches does not mean that its kernel has to be multiplied with each appearance (so that KB appears only once and not four times in the products).
In summary, then, the minimum number of universes in the multiverse, N, is given by the product of the kernels of all of the quantum events in the universe (which may be determined by inspection of diagrams like Figure 2). This means, of course, that the number of universes for every event has components of kernels of events in completely different branches of the multiverse. Hence, for instance, the twig containing outcome B1 in universe (1) includes the kernel for event C in its product (KA1 KB1 KC), although C occurs in a completely separate branch. Indeed, the number of universes containing any quantum event in the multiverse contains components of the kernels for every quantum event in the multiverse. As we shall see in The Finite Multiverse, from this we can conclude that the multiverse is finite.
Click here to go to The Finite Multiverse [15]
